[Day 149] Learning about the Origin-Destination Matrix Prediction problem in passenger prediction tasks

 Hello :)
Today is Day 149!


A quick summary of today:
  • back in the lab and read 2 papers about Origin-Destination Matrix Prediction via Graphs


I decided to start using obsidian to take notes and it is amazing. It is also good practice writing math using latex. Also for some reason I cannot copy paste the math formulas, so some of the text below is in pictures so that the formula (math notation) can be included for clarity. I need to figure out a way to better share these notes. 


Paper 1: Gallat - Passenger Mobility Prediction via Representation Learning for Dynamic Directed and Weighted Graph (DDW)

Introduction

At first, studies concentrated on passenger demand as a function of starting location and time period. However, this failed to account for the passengers' destination. This was tackled by the definition of Origin-Destination Matrix prediction problems, where there are different time slots with their own OD matrix describing travel demand from region i to region j. Based on this ODMP, Graph Neural Networks have emerged as the go-to solution because of their ability to capture complex relationships and compared to previously applied CNNs, generalise to non-Euclidean graph topologies. 


Definitions


Methodology



  • pre-weighted functions - helps with the data sparsity. In addition to node semantic similarity, the obtained weights also incorporate real-time popularity of neighbour regions

Temporal Attention Layer

This layer can capture the sequential dependencies among embeddings and generate spatiotemporal representation for predicting the passenger demand in the next time slot. A naive approach to this would be to gather information from P most recent and consecutive DDW graphs. This might not work that well since in reality, a graph at time T will have similarity with graphs in close time slots, and if the time difference is too big this will introduce noise into the learned graph representation. To improve on that, the paper uses P historical DDW graphs form the same time slow of each day.

Transferring Attention Layer

Focusing on the next time slot, we can predict passenger demands between regions. Initially a vector with outbound passenger demands at the next time slot T+1 is created. Then it is distributed to different regions using a probability distribution that indicates the likelihood of a passenger trip from one region to every other region in the next time slow.


Experiment

Dataset


Baseline models

History Average (HA), LSTNet, GCRN, GEML

Results

0,3,5 are thresholds for demand. I.e. threshold 0 includes all regions, threshold 3 includes regions where there is at least 3 passenger demands 


Paper 2: GEML - Origin-Destination Matrix Prediction via Graph Convolution. A New Perspective of Passenger Demand Modeling

Introduction

The ODPM problem is essential to solve for large taxi companies, as it will give information about customers' demands from one place to another. ODPM provides info about combinations of different origins and destinations, and the demand for each origin-destination combination. The target is to predict the number of orders from one place to another in a given time slot.

OD matrix construction



Methodology


Grid-Embedding based Multi-task Learning (GEML) 

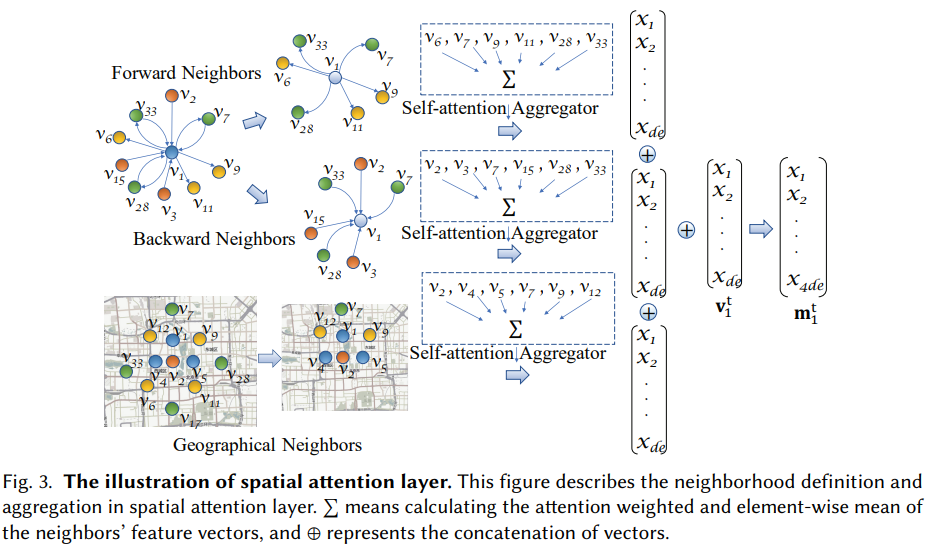
OD matrices are extracted from mobility records of ride service providers. Then the grid embedding part of GEML learns the embedding vector for each grid through aggregating geographical and semantic neighbours information. Next, the vector representation is put through a multi-task neural network which learns the grid for the most recent time slot. Finally, the result is used to for a predicted OD matrix. In the authors' proposed model, both spatial information - using a neighbour-based grid embedding to learn each grid's representation by aggregating neighbour information, and temporal information - using the multi-task neural network that can learn dynamic trends of passenger movement over time, is captured.

Grid embedding

GCNs are limited when it comes to sparse graphs - which can happen in low demand areas. To tackle this, the authors propose two kinds of neighbourhoods for better neighbourhood aggregation - geographical and semantic neighbours. This achieves to measure the closeness between a grid and its neighbours and in addition, the traffic flow's semantic strength between origin and destination.




Evaluation

Compared with History Average (HA), LSTM, LSTNet, GCRN 
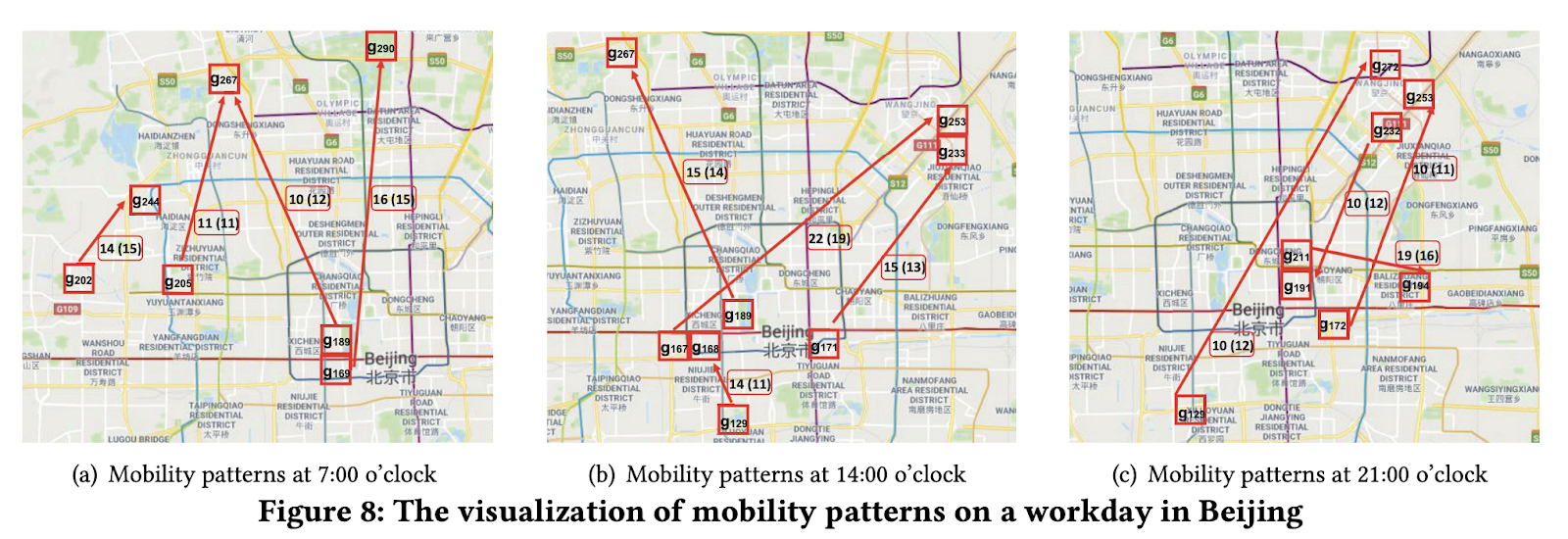
Where GEML-XX are modifications to the model.


Visualisation

(a) Morning mobility: people leave home and go to different destinations. g202, g205, g189, g169 are residential areas, while g267, g290 are software parks

(b) Post-lunch mobility: there are still many passengers going to work/entertainment venues.

(c) Evening mobility: there are people going home, but also going to entertainment venues



That is all for today!

See you tomorrow :)

Popular posts from this blog

[Day 198] Transactions Data Streaming Pipeline Porject [v1 completed]

Image
 Hello :) Today is Day 198! A quick summary of today: data streaming pipeline project [v1 done] Here is a link to the project's repo. Well ... I did not know I can do it in a day (~14 hours) after yesterday's issues but here we are. Turns out in order to insert the full (~70 variables with nested/list structure), I need the proper pyspark schema. And yesterday I did not have that and that is why when I was reading data in the kafka producer I was getting NULL in the columns - my schema was wrong. Well today I not only fixed the schema for the 4 variables I had yesterday, but included *all* the variables that come from the Stripe API ~ 70 (for completeness).  When I run docker-compose, the data streams and is input into the postgres db (and is still running). Unfortunately, the free Stripe API for creating realistic transactions has a limit of 25, so every 3 seconds, 25 new transactions are sent to the db. It has been running half the day (since I got that set up) and as I am wr
Read more

[Day 107] Transforming natural language to charts

Image
 Hello :) Today is Day 107! A quick summary of today: created text2chart - transforming natural language to charts [ github ] [ webapp ] I am super sick, but in the around 3 hours of my fever not being high, I managed to study a bit. I was again thinking about creating some nlp project but was stuck on the idea of how to host a model. After looking around I found this article where they create a similar app called chat2vis  and they use codellama. I know codellama is an open source model that I can get from huggingface and I wondered, how did they host it. Turns out - they ask the user to input a huggingface api key, which then allows for querying and generating content. (AWESOME! this is applicable to some of the other PDF chat apps that I have, but I will look to make an app of them later).  My fever eased a bit, and I sat on my chair to do some work ^^ Here is a breakdown of the app. I used streamlit. Also, 2 default datasets during dev: Financial Statements of Major Companies(2009-
Read more

[Day 54] I became a backprop ninja! (woohoo)

Image
 Hello :) Today is Day 54! A quick summary of today: Read through cs231n's neural network lectures [1] [2] [3] Spent 8 hours going over Andrej Karpathy's backprop ninja tutorial After yesterday's confidence boost in doing backprop, I came in today with the intention of becoming of, as Andrej Karpathy calls it, a backprop ninja.  The cs231n NN lectures were the usual about how NN became to be, param initialization, activation functions, loss functions, regularization and optimizers. Nothing out of the ordinary, but still was good to reassure myself of that knowledge. But that was definitely not the main even of today. As I mentioned, I wanted to become (or at least attempt to become) a backprop ninja today. I have watched that particular tutorial twice, the 1st time I had no idea what is going on, the 2nd time I could follow, and now it was the 3rd time - and now, I wanted to participate and actually see the why and the how of the things we have to do, when we do manual back
Read more