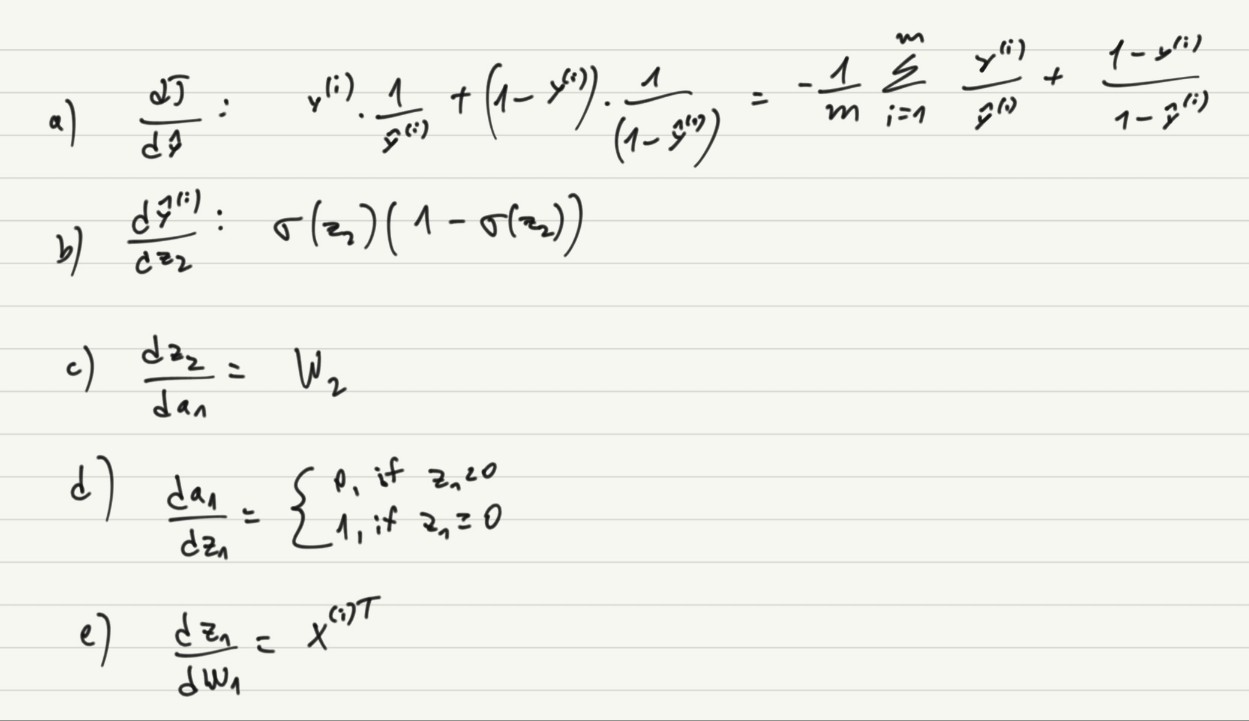[Day 53] Getting closer to becoming a 'backprop ninja' (thanks to Stanford Uni's cs231n assignments)

 Hello :)
Today is Day 53!

A quick summary of today
Started Stanford University's cs231n, and today I covered:

• Image Classification: Data-driven Approach, k-Nearest Neighbor, train/val/test splits

• Linear classification: Support Vector Machine, Softmax

• Optimization: Stochastic Gradient Descent

• Backpropagation, Intuitions

First I will quickly share my notes from the 1st three, and then for the big one (backprop) - will do it last.

1st lecture - Image classification using KNN

Actually my impression is not so much from the theory in the lecture, but from the assignment exercises which the course has. 

The KNN assignment was about implementing the loss of KNN (L1/L2 distance) and how to do it efficiently. 

Firstly there was the most inefficient one - with two for loops

Then it was with one for loop

And then, the most efficient one which uses matrix multiplication magic

I have never implemented knn by myself so this was a nice challenge.

Also all 3 were compared and the results are:

- Two loop version took 297.302739 seconds

- One loop version took 306.791257 seconds

- No loop version took 0.973995 seconds

Also after using the distance formula, it code showed me a distance map which was quite interesting in that it shows some rows where the distance is brighter and some is darker (whiter and blacker)

Turns out the explanation is that bright rows are caused by the test img being different vs train - if the test is very different from train, we get a bright row. Whereas bright columns are caused by the train image being very dif from the test image, so we end up with bright columns. 

2nd lecture: Linear classification: SVM and softmax

Here I learned about Multiclass SVM loss versus the softmax for the image classification. And I understood the formulas for both. I knew the softmax (cross-entropy) loss, but the multiclass SVM loss was new to me. 

It is the sum of max between 0 and the difference where the labels are different and some delta which controls how strict the classification should be, and then a regularization loss. But when I saw the implementation (below) I was a bit lost.

Ok, side note. I just wrote the above sentence and my head told me I cannot leave it like this. So I went on google to search for the implementation in code (in a vectorized way) so that I can understand it. And I actually found this, which has nice comments and helps me understand what is going on haha. 

The only bit that is tricky right now is the y_hat_true line and why do we need to create it in that way. But I can explore that tomorrow.

3rd lecture: Optimization: Stochastic Gradient Descent 

This was just how gradient descent work and it did not have a particular exercise to it.

4th lecture: Backpropagation

We finally reached the most exciting part of my day. As I was reading through the lecture, I was thinking "oh, will I be implementing every step of forward and backprop in a neural network similar to Andrej Karpathy's 'become a backprop ninja video' ?' well it turns out the answer is yes. And it was really exciting to do it a slow steady manner. 

The lecture went over derivative rules that we all know and love

+ for sigmoid's derivative is (1-sigmoid(x))*sigmoid(x)

Also, I did not know but the derivate when going through a max gate is

The lecture showed short graphs like:

and this motivated me to do something similar by hand. And so I did.

I hope the image is clear when zoomed in, but I just wanted to go back on a simple neural network + the sigmoid. 

Also found this exercise:

For the below 2 layer neural netowork, write out the derivatives

Not gonna lie - it felt good knowing that I know these things. 

At the end of the lecture there was this paper about Vector, Matrix, and Tensor Derivatives by Erik Learned-Miller. It explains in a very simple way, what is happening when we multiply vectors and matrices and how the size should align when we want to do matrix multiplication or other operations.

And with this knowledge from the short explanation paper and my confidence in the bag, I went onto the exercise assignment of the lecture which requires me to create forward and backward of a 2 layer neural network in code.

First, the forward function:

A big fear and a reason of not knowing what is happening was because of not knowing the shapes when we do matrix multipication, and when I watch someone do it, I am not sure why they do it, why do they change the shape of some matrix? Well in the codes below, I did a lot of prints figuring out how and why. 

Backward function

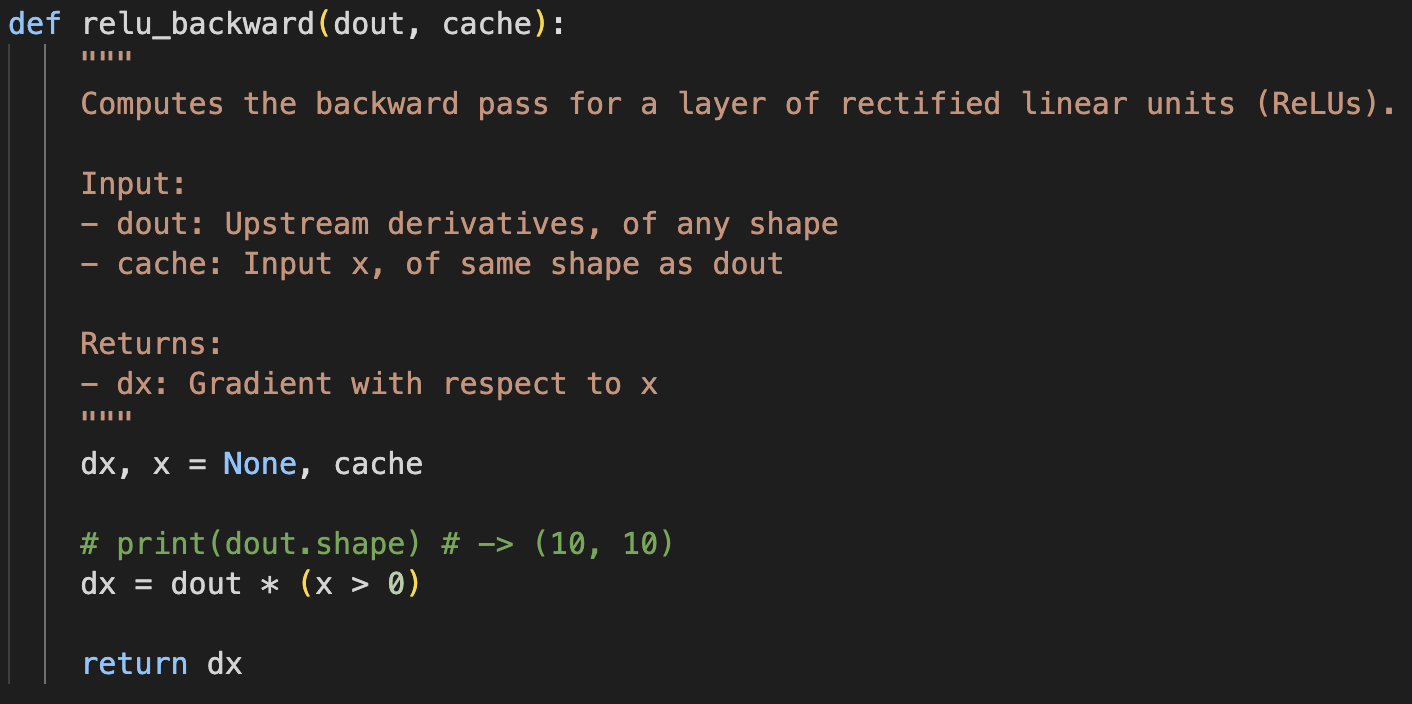
Relu forward:

Relu backward:

In the exercises there are parts about batch norm, layer norm, dropout, conv, maxpool, and softmax - all forward and backward.

So exciting! I feel I am getting closer to becoming a, as Andrej Karpathy calls it, backprop ninja.

That is all for today!

See you tomorrow :)